Fourier Space Time-stepping (FST) framework is a generic framework based on the Fourier transform for pricing and hedging of various options in equity, commodity, currency, and insurance markets. The pricing problem can be reduced to solving a partial integro-differential equation (PIDE). The FST framework circumvents the problems associated with the existing finite difference methods by utilizing the Fourier transform to solve the PIDE, with resulting method being highly efficient and rapidly convergent.
The Fourier transform can be applied to the pricing PIDE to obtain a linear system of ordinary differential equations that can be solved explicitly. Solving the PIDE in Fourier space allows for the integral term to be handled efficiently and avoids the asymmetrical treatment of diffusion and jump terms arising in the finite difference schemes found in literature. For path-independent options, prices can be obtained for a range of stock prices in one iteration. For exotic, path-dependent options, a time-stepping algorithm is developed to handle barriers, free boundaries, and exercise policies.
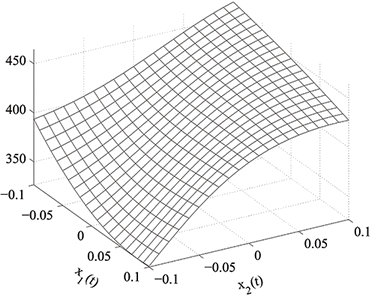
The FST framework-based methods are applied to a wide range of option pricing problems. Pricing of single- and multi-asset, European and path-dependent options under independent-increment exponential Levy stock price models, common in equity and insurance markets, can be done efficiently via the cornerstone FST method. Mean-reverting Levy spot price models, common in commodity markets, are handled by introducing a frequency transformation, which can be readily computed via scaling of the option value function.
The Fourier Space Time-stepping (FST) project is based upon research conducted by Kenneth R. Jackson, Sebastian Jaimungal and Vladimir Surkov at University of Toronto. The MATLAB code has been written by Vladimir Surkov and is available on SourceForge. Below is the description of the four files available:
- Option pricing under independent-increment jump-diffusion and Levy models for equity derivatives (FST)
For more details see the paper Fourier Space Time-stepping for Option Pricing with Levy Models  and download the code 
- Option pricing under mean-reverting jump-diffusion models for commodity derivatives (mrFST)
For more details see the paper Levy Based Cross-Commodity Models and Derivative Valuation and download the code
- Option pricing under mean-reverting jump-diffusion models for interest rate derivatives (irFST)
For more details see the paper Valuing Early Exercise Interest Rate Options with Multi-Factor Affine Models and download the code
- Computation of option Greeks (greekFST)
For more details see the paper Efficient Construction of Robust Hedging Strategies under Jump Models and download the code
|
